فصل اول - بخش اول : مجموعه ها(مجموعه مرجع و اجتماع دو مجموعه و ...)
تعریف مجموعه : به تعدادی از اشیاء، اعداد ، افراد ، مشخص که گروهی را
تشکیل بدهند و رو به دوازدهم متمایز باشند مجموعه می گویند. هر یک از اشیاء
، افراد، اعداد یک مجموعه یک عضو مجموعه نامیده می شوند.
N= مجموعه اعداد طبیعی
z= مجموعه اعداد صحیح (مثبت، منفی و صفر)
Q= مجموعه اعداد گویا
R= مجموعه اعداد حقیقی
************************************************************
نمایش یک مجموعه :
روش های گوناگونی برای مشخص کردن یک مجموعه وجود دارد . درهمه ای روش ها
باید دقیقاً مشخص شود که چه اشیایی عضو مجموعه اند و یا چه چیزهایی عضو
مجموعه نیستند.
عضو یک مجموعه :
هر یک از اشیایی که مجموعه را تشکیل می دهند یک عضو آن مجموعه است و اگر
a عضوی مجموعه A باشد می نویسند a€A ولی می خوانند در aمتعلق به Aاست. و
اگر bعضوی مجموعه A نباشد می نویسند و می خوانند b متعلق به A نیست یا b
عضو A نیست.
مجموعه تهی :
مجموعه ای که هیچ عضو نداشته باشد به آن مجموعه تهی می گویند و با نماد {} با نشان می دهند.
مجموعه های مساوی :
هر گاه هر یک از عضوهای مجموعه A متعلق به مجموعه B و هر یک از اعضاء
مجموعه B متعلق به مجموعه A می باشد در این صورت گفته می شود A=B در غیر
این صورت گفته می شود A ≠ B نامیده می شود مانند{A={20,3,5,70 و
{B={3,2,5,70 که A=B است ولی می باشد.
 .
.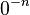 تعریف نشدهاست، زیرا تقسیم بر صفر وجود ندارد.
تعریف نشدهاست، زیرا تقسیم بر صفر وجود ندارد.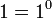 . (هر عدد به توان صفر می شود یک )
. (هر عدد به توان صفر می شود یک ) تعریف نشدهاست. ( زیرا هر عدد به توان صفر می شود یک & صفر به توان هر عدد می شود صفر # تناقض)
تعریف نشدهاست. ( زیرا هر عدد به توان صفر می شود یک & صفر به توان هر عدد می شود صفر # تناقض)